空間図形(発展)

図のような底面の半径が4cmの円錐を、頂点Oを中心として平面上で転がしたところ、図に斜線で示した円の上を1周して戻るまでに4回転半した。

(1) この円錐の母線の長さは何cmか

(2) この円錐の表面積を求めよ。

右の図のように１辺の長さが12cmの正方形ABCDがある。M,Nはそれぞれ辺BC,CDの中点である。AM,AN,MNを折り目として立体を作ると三角錐ができる。

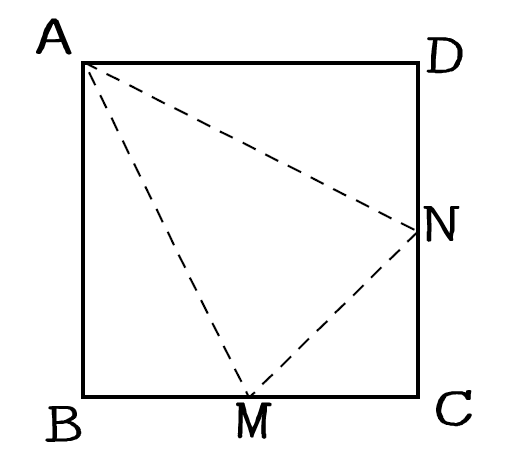
(1) この三角錐の体積を求めよ。

(2) △AMNを底面としたときのこの三角錐の高さを求めよ。

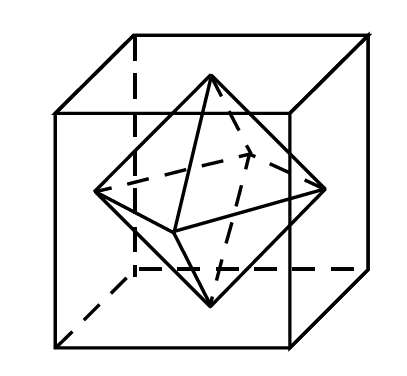
右の図のように１辺の長さが6cmの立方体がある。この立方体の各面の対角線の交点を頂点として作られる正八面体の体積を求めよ。

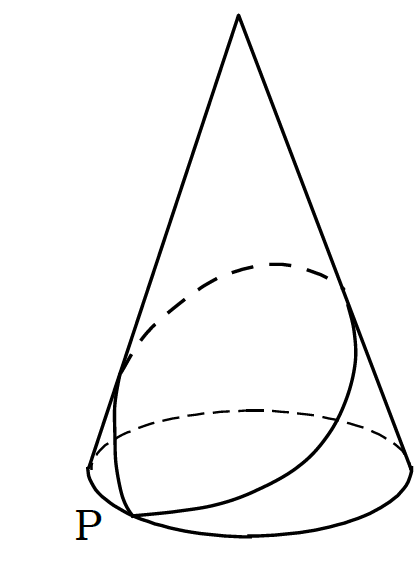
図の円錐は底面の半径3cm,母線の長さ18cmである。点Pから側面を通り一周して戻ってくるときの最短の道のりを求めよ。

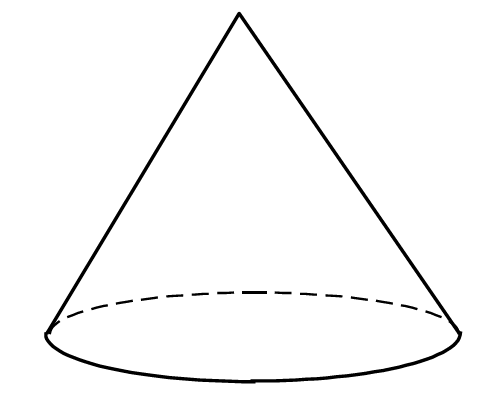
図の円錐は底面の半径が5cm,表面積が60πcm²である。この円錐の母線の長さを求めよ。

右の図のサッカーボールは、12個の正五角形と20個の正六角形の合わせて32面でできた多面体である。どの頂点にも１個の正五角形と２個の正六角形の面が集まっている。

(1) この多面体の辺は何本あるか。

(2) この多面体の頂点はいくつあるか。